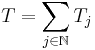Cotlar–Stein lemma
In mathematics, in the field of functional analysis, the Cotlar–Stein almost orthogonality lemma is named after mathematicians Mischa Cotlar and Elias Stein. It may be used to obtain information on the operator norm on an operator, acting from one Hilbert space into another when the operator can be decomposed into almost orthogonal pieces. The original version of this lemma (for self-adjoint and mutually commuting operators) was proved by Mischa Cotlar in 1955[1] and allowed him to conclude that the Hilbert transform is a continuous linear operator in 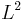 without using the Fourier transform. A more general version was proved by Elias Stein.[2]
without using the Fourier transform. A more general version was proved by Elias Stein.[2]
Cotlar–Stein almost orthogonality lemma
Let 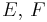 be two Hilbert spaces. Consider a family of operators
be two Hilbert spaces. Consider a family of operators  ,
, 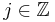 , with each
, with each 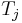 a continuous linear operator from
a continuous linear operator from  to
to  .
.
Denote
The family of operators 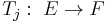 ,
, 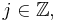 is almost orthogonal if
is almost orthogonal if
The Cotlar–Stein lemma states that if 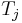 are almost orthogonal, then the series
are almost orthogonal, then the series 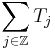 converges in the strong operator topology, and that
converges in the strong operator topology, and that
Example
Here is an example of an orthogonal family of operators. Consider the inifite-dimensional matrices
and also
Then 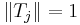 for each
for each  , hence the series
, hence the series 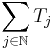 does not converge in the uniform operator topology.
does not converge in the uniform operator topology.
Yet, since 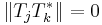 and
and 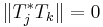 for
for 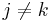 , the Cotlar–Stein almost orthogonality lemma tells us that
, the Cotlar–Stein almost orthogonality lemma tells us that
converges in the strong operator topology and is bounded by 1.


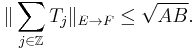
![T=\left[
\begin{array}{cccc}
1&0&0&\vdots\\0&1&0&\vdots\\0&0&1&\vdots\\\cdots&\cdots&\cdots&\ddots\end{array}
\right]](/2012-wikipedia_en_all_nopic_01_2012/I/dd5e0118217249d3a0f5b7355eef0b0d.png)
![\qquad
T_1=\left[
\begin{array}{cccc}
1&0&0&\vdots\\0&0&0&\vdots\\0&0&0&\vdots\\\cdots&\cdots&\cdots&\ddots\end{array}
\right],
\qquad
T_2=\left[
\begin{array}{cccc}
0&0&0&\vdots\\0&1&0&\vdots\\0&0&0&\vdots\\\cdots&\cdots&\cdots&\ddots\end{array}
\right],
\qquad
T_3=\left[
\begin{array}{cccc}
0&0&0&\vdots\\0&0&0&\vdots\\0&0&1&\vdots\\\cdots&\cdots&\cdots&\ddots\end{array}
\right],
\qquad
\dots.](/2012-wikipedia_en_all_nopic_01_2012/I/abff3b6cac0a98f0f763d50d8d0ae0a8.png)